Table 3.8 shows the command line options specific to MImapqtl.
If you choose to begin analysis from some initial model, it should be formatted as an
Rqtl output file and specified with the -E option. For data sets with
multiple traits, you can specify the trait to analyze with the -t option.
If the specified trait is 0, then all traits whose names begin with a plus sign (![]() )
will be analyzed (one at a time). If the specified trait is larger than the number of
traits, then all traits will be analyzed one at a time, unless their names begin with a
minus sign (
)
will be analyzed (one at a time). If the specified trait is larger than the number of
traits, then all traits will be analyzed one at a time, unless their names begin with a
minus sign (![]() ).
).
You may specify a maximal number of QTL and epistatic interactions to fit in the model.
The limitations of C on a 32 bit computer mean that you can only fit up to 19 QTL
in a cross with three marker genotypes (SFx and RFx lines). Thus, 19 will be a hard limit on
the number of loci at this time. In practice, it is not wise to try to fit more than
![]() parameters, where
parameters, where ![]() is the sample size. Thus, MImapqtl will automatically
adjust this number so that it is no greater than
is the sample size. Thus, MImapqtl will automatically
adjust this number so that it is no greater than ![]() for backcrosses and recombinant inbred lines,
for backcrosses and recombinant inbred lines,
![]() for lines with three marker genotypes (since each QTL has an additive and a dominance effect).
Once main effects are fitted for the QTL, MImapqtl searches for epistatic effects. Again,
it will only try to fit up to
for lines with three marker genotypes (since each QTL has an additive and a dominance effect).
Once main effects are fitted for the QTL, MImapqtl searches for epistatic effects. Again,
it will only try to fit up to ![]() parameters so only
parameters so only ![]() minus the number of main
effects will be fitted. For example, if you have a sample size of 400, then
minus the number of main
effects will be fitted. For example, if you have a sample size of 400, then
![]() For an
SF2 line, if you find 10 QTL, then 20 parameters have been fitted (10 additive and 10 dominance effects).
Thus, there will be up to
For an
SF2 line, if you find 10 QTL, then 20 parameters have been fitted (10 additive and 10 dominance effects).
Thus, there will be up to ![]() possible epistatic effects that can be fitted.
possible epistatic effects that can be fitted.
The walking speed is identical to that in Zmapqtl and JZmapqtl and is used during the refinement of QTL positions and the search for new QTL. For the refinement of QTL position, for each QTL, the position is moved within the QTL interval from one end to the other and an information criterion is calculated for each position. The minium over the interval is the best position for the QTL.
The information criterion is is a function of the likelihood ratio and the number of parameters
that gives an indication of how good the model fits the data. This is a function in form
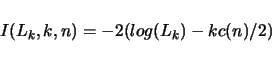
Use the numbers above with the -S option to indicate which information criterion
you want to use. When comparing a model with ![]() parameters to one with
parameters to one with ![]() parameters,
if
parameters,
if
![]() is greater than the threshold value specified with the -L
option, then the parameter is considered significant. During a scan over the entire genome,
if the maximum of
is greater than the threshold value specified with the -L
option, then the parameter is considered significant. During a scan over the entire genome,
if the maximum of
![]() is greater than the threshold, then that position
parameter is retained. A non-zero penalty function supersedes the requirement of a true threshold.
Therefore, if using one of the first five penalty functions, you can use a threshold of 0.0.
For function six (that is, no penalty), it is best to do a permuation test to determine the initial threshold.
is greater than the threshold, then that position
parameter is retained. A non-zero penalty function supersedes the requirement of a true threshold.
Therefore, if using one of the first five penalty functions, you can use a threshold of 0.0.
For function six (that is, no penalty), it is best to do a permuation test to determine the initial threshold.
In general, it is probably best to start with information criterion 1 with a threshold of 0.0. We have done some initial simulations to support the utility of this approach. If no QTL are identified using information criterion 1, then one could use no penalty function and do a permutation test for the threshold.