Qstats

Qstats is a good place to start in analyzing your data. It computes some basic statistics on the quantitative traits and summarizes missing data. Let $\{ y_1, y_2, \cdots, y_n \}$ be a vector of quantitative trait values. For each trait in turn, it calculates the sample size (n), mean ( $\bar{y} = \frac{1}{n}\sum_1^n y_i$), variance ( $s^2=\frac{1}{n-1}\sum_1^n (y_i-\bar{y})^2$), standard deviation ( $s = \sqrt{s^2}$), skewness, kurtosis and average deviation, $\frac{1}{n} \sum_{i=1}^n \vert y_i - \bar{y}\vert$. The coefficient of variation is the sample standard deviation divided by the sample mean.

lynchwalsh@98 provide a lucid explanation of some of the statistics calculated by Qstats. Let the $k$th sample moment be $M(k) = \frac{1}{n} \sum_{i=1}^n y_i^k$. Clearly, $M(1) = \bar{y}$. Using the notation $\bar{y^k} = M(k)$, we can estimate the sample variance with

$$s^2 = \frac{n}{n-1}(\bar{y^2} - \bar{y}^2)$$ (3.1)

An estimate of the skewness is

$$Skw(y) = \frac{n^2}{(n-1)(n-2)}(\bar{y^3} - 3 \bar{y^2} \bar{y} + 2 \bar{y}^3)$$

The standard error of skewness depends on the underlying distribution but can be approximated by $\sqrt{6/n}$. The coefficient of skewness, $k_3$ is

$$k_3 = \frac{Skw(y)}{s^3}$$

where the sample standard deviation, $s=\sqrt{s^2},$ is estimated from (3.1). Kurtosis is estimated by

$$Kur(y) = \frac{n^2(n+1)}{(n-1)(n-2)(n-3)}(\bar{y^4} - 4\bar{y^3}\bar{y} + 6\bar{y^2}\bar{y}^2 - 3\bar{y}^4)$$

and the coefficient of kurtosis is

$$k_4 = \frac{Kur(y) - 3 s^4}{s^4}$$

Like skew, the standard error of kurtosis is dependent upon the population distribution. We give the estimate $\sqrt{24/n}$. A test of normality for the vector $y$ then involves the test statistic

$$S = \frac{n k^2_3}{6} + \frac{n k^2_4}{24}$$

which is distributed as a $\chi^2$ with two degrees of freedom. The critical values for the rejection of normality are 5.99 and 9.21 for tests at the 5% and 9% levels, respectively.

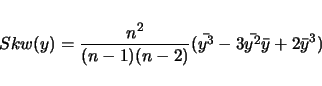
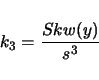
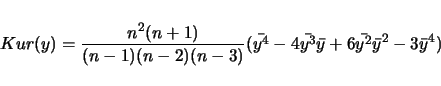
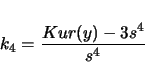
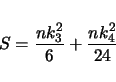
An example of the output follows:

 ------------------------------------------------------
 ------------------------------------------------------
 	This is for -trait 1 called szfreq
 ------------------------------------------------------
 		Sample Size................           119
 		M(1).......................        0.4349
 		M(2).......................        0.2184
 		M(3).......................        0.1195
 		M(4).......................        0.0694
 		Mean Trait Value...........        0.4349
 		Variance...................        0.0295
 		Standard Deviation.........        0.1718
 		Coefficient of Variation...        0.3951
 		Average Deviation..........        0.1398
 		Skw..LW(24)................       -0.0010
 		.....Sqrt(6/n).............        0.2245
 		Kur..LW(29)................        0.0022
 		.....Sqrt(24/n)............        0.4491
 		k3...LW(24)................       -0.1922
 		k4...LW(28)................       -0.5250
 		S (5%: 5.99, 1%: 9.21).....        2.0992
 ------------------------------------------------------
 ------------------------------------------------------

In the above example, LW(i) refers to a page number in lynchwalsh@98 where one can find an explanation of the quantity. The value of the test statistic $S$ is 2.0992, thus one would fail to reject the hypothesis that this trait is normally distributed.

After the basic statistics, Qstats draws a histogram of the quantitative trait. It is a simple histogram in that the range of the data are divided into 50 equally sized bins, and the number of data points falling into each bin are counted and plotted. A small table following the histogram gives the sample size, minimum, first quartile, median, second quartile and maximum.