




Next: Permutation Test output
Up: Zmapqtl
Previous: Permutations, Bootstraps and Jackknives
Contents
Index
Output
Here is a truncated example of the output of Zmapqtl for a backcross.
# 890840384 -filetype Zmapqtl.out
#
# QTL Cartographer V. 1.13b, March 1998
# This output file (qtlcart.z) was created by Zmapqtl...
#
# It is 10:39:44 on Wednesday, 25 March 1998
#
#
#The position is from the left telomere on the chromosome
-window 10.00 Window size for models 5 and 6
-background 5 Background parameters in model 6
-Model 6 Model number
-trait 1 Analyzed trait [Trait_1]
-cross B2 Cross
# Test Site * Like. Ratio Test Statistics * Additive
c m position H0:H1 R2(0:1) TR2(0:1) H1:a S1
-s
1 1 0.0001 0.411 0.002 0.473 0.027 1.531
1 2 0.0133 0.016 0.000 0.472 0.005 1.542
1 2 0.0333 0.023 0.000 0.472 0.006 1.547
1 2 0.0533 0.031 0.000 0.472 0.008 1.554
1 2 0.0733 0.041 0.000 0.472 0.009 1.563
1 2 0.0933 0.052 0.000 0.472 0.010 1.572
1 2 0.1133 0.063 0.000 0.472 0.011 1.582
1 2 0.1333 0.073 0.000 0.472 0.012 1.593
.
.
.
-e
For a backcross, let 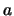 be the additive effect. We have two hypotheses:
be the additive effect. We have two hypotheses:
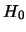 : no QTL effect at the test position, i.e.
: no QTL effect at the test position, i.e. 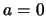
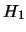 : There is a QTL effect at the test position, i.e.
: There is a QTL effect at the test position, i.e. 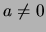
The first eight columns correspond to
- Chromosome of test position
- Left flanking marker of test position
- Absolute position from left telomere, in Morgans.
- Likelihood ratio test statistic for
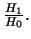 It is a
It is a 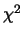 random variable with one degree of freedom for any position, meaning that a
value of 3.84 or higher is evidence for a QTL. The significance level over more
positions will be higher due to multiple testing.
random variable with one degree of freedom for any position, meaning that a
value of 3.84 or higher is evidence for a QTL. The significance level over more
positions will be higher due to multiple testing.
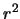
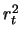
- Estimate of
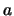 (the additive effect) under
(the additive effect) under 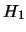
- Test statistic
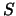 for the normality of the residuals under
for the normality of the residuals under 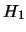
The last 13 columns are not shown because they are only valid for 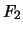 design experiments.
They would all be zeros if shown.
design experiments.
They would all be zeros if shown.
The output for an 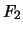 design (or any design in which dominance effects can be estimated)
is similar, but has more information.
For an
design (or any design in which dominance effects can be estimated)
is similar, but has more information.
For an 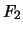 , you can estimate additive (
, you can estimate additive (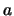 ) and dominance (
) and dominance (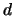 ) parameters at each
position. Thus, there are four hypotheses.
) parameters at each
position. Thus, there are four hypotheses.
and twelve full columns of output, corresponding to all possible hypothesis tests
and parameter estimates.
The 21 columns correspond to
- Chromosome of test position.
- Left flanking marker of test position.
- Absolute position from left telomere, in Morgans.
- Likelihood ratio test statistic for
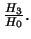
- Likelihood ratio test statistic for
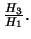
- Likelihood ratio test statistic for
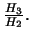
- Estimate of
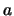 (the additive effect) under
(the additive effect) under 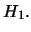
- Estimate of
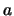 (the additive effect) under
(the additive effect) under 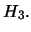
- Estimate of
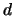 (the dominance effect) under
(the dominance effect) under 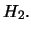
- Estimate of
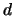 (the dominance effect) under
(the dominance effect) under 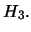
- Likelihood ratio test statistic for
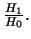
- Likelihood ratio test statistic for
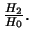
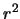 for
for
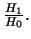
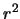 for
for
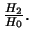
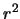 for
for
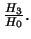
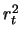 for
for
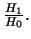
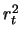 for
for
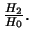
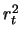 for
for
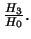
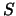 for
for 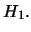
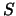 for
for 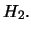
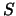 for
for 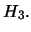
Subsections





Next: Permutation Test output
Up: Zmapqtl
Previous: Permutations, Bootstraps and Jackknives
Contents
Index
Christopher Basten
2002-03-27
![]() be the additive effect. We have two hypotheses:
be the additive effect. We have two hypotheses:
![]() design (or any design in which dominance effects can be estimated)
is similar, but has more information.
For an
design (or any design in which dominance effects can be estimated)
is similar, but has more information.
For an ![]() , you can estimate additive (
, you can estimate additive (![]() ) and dominance (
) and dominance (![]() ) parameters at each
position. Thus, there are four hypotheses.
) parameters at each
position. Thus, there are four hypotheses.